Autokey Cipher
The Autokey cipher was invented by Vigenère in 1586. Since computers ceased to exist then, many ciphers in our modern time are extremely vulnerable to brute force attacks. While it reamins more sophisticated than more known ciphers like the Caesar Cipher, the two ciphers have the brute force asymptotic complexity of \(O(n)\) where \(n\) is the number of characters in the alphabet. Fortunately, this cipher avoids the vulnerability of Vigenère cipher(Another cipher invented by Vigenère). Kasiski's Method analyzes the distribution of characters in the encrypted string and generates the index of confidence.
\[\binom{f_i}{2} = \frac{f_i \left(f_i-1\right)}{2}\]
The end result is elementary combinatorics, but if you want to learn more about Kasiski Method, you can read more about it here.
Encryption
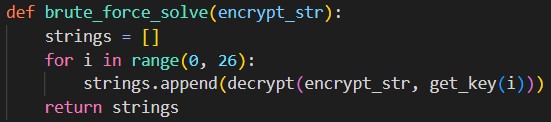
Now let's talk about how Autokey Cipher is implemented. First, we must define the alphabet of characters we will use. For our purpose, we will use the 26 characters of the English alphabet where "a"=0 and "z"=25. Then a value will be assigned to each character. This can be done with a dictionary. Next, We have our plaintext, which we wish to encrypt, and a seed(A key for our encryption) represented as follows: \(E\) (encrypted string), \(P\) (plain text), and \(S\) (seed).
\begin{align*} E_i &\equiv P_i + S_i \mod 26 \\ S_{i+1} &= P_i \end{align*}
This algorithm proceeds until \(i=n\) where n is the length of the string. On the last value, the seed value generated will be irrelevant.
To best illustrate the algorithm, it's best to show an example.
Let our plain text be "hello," and our seed is "w." This results in [7, 4, 11, 11, 14] for "hello," and 22 for our "w."
\begin{align*} E_1 &\equiv P_1 + S_1 \mod 26 \\ E_1 &\equiv 7 + 22 \equiv 3 \mod 26 \\ \end{align*} \begin{align*} E_2 &\equiv P_2 + S_2 \mod 26 \\ E_2 &\equiv 4 + 7 \equiv 11 \mod 26 \\ \end{align*} \begin{align*} E_3 &\equiv P_3 + S_3 \mod 26 \\ E_3 &\equiv 11 + 4 \equiv 15 \mod 26 \\ \end{align*} \begin{align*} E_4 &\equiv P_4 + S_4 \mod 26 \\ E_4 &\equiv 11 + 11 \equiv 22 \mod 26 \\ \end{align*} \begin{align*} E_5 &\equiv P_5 + S_5 \mod 26 \\ E_5 &\equiv 14 + 11 \equiv 25 \mod 26 \\ \end{align*}
The end result is the encrypted string "dlpwz." This can be done with the following code segment:
Decryption
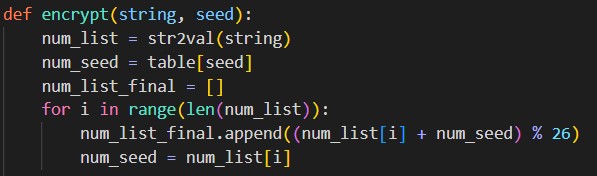
Now let's decrypt the string "dlpwz" which is [3, 11, 15, 22, 25]. We will use the same seed and cipher text.
\begin{align*} P_1 &\equiv E_1 - S_1 \mod 26 \\ P_1 &\equiv 3 - 22 \equiv 7 \mod 26 \\ \end{align*} \begin{align*} P_2 &\equiv E_2 - S_2 \mod 26 \\ P_2 &\equiv 11 - 7 \equiv 4 \mod 26 \\ \end{align*} \begin{align*} P_3 &\equiv E_3 - S_3 \mod 26 \\ P_3 &\equiv 15 - 4 \equiv 11 \mod 26 \\ \end{align*} \begin{align*} P_4 &\equiv E_4 - S_4 \mod 26 \\ P_4 &\equiv 22 - 11 \equiv 11 \mod 26 \\ \end{align*} \begin{align*} P_5 &\equiv E_5 - S_5 \mod 26 \\ P_5 &\equiv 25 - 11 \equiv 14 \mod 26 \\ \end{align*}
This results back in our original string "hello." This operation can be performed by the following code.
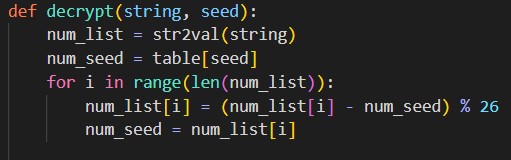
Brute Force Attack
Since this cipher was designed to avoid easy interception in the 16th century, there are only \(n\) possible strings where \(n\) is the number of characters in the alphabet. In our alphabet, there were only 26 characters. Evidently, after 26 iterations, the string can be found. This issue persists as Unicode only has 149,186 characters, far too small to be considered secure with computers. One issue that may arise is that multiple correct meanings may form when the alphabet expands, but this is not a problem for the Autokey Cipher as the plain text size increases. The Autokey Cipher has the advantage that the encryption type is not public(as opposed to public key encryption). The disadvantage is that if the attacker discovers the encryption type, the message is easily readable. The brute force algorithm can be viewed below.