Tower of Hanoi

History of Problem

The Tower of Hanoi problem was invented by French mathematican Édouard Lucas. It was a legend that Hindu temples used the excercise to improve the mental discpline of young priests. For more info, read Scientific American.

Problem Statement

Given \(n\) rings on rod A, where the ring strictly decrease in size, give a sequence of steps (moving the top ring on a rod to another rod) such that all \(n\) rings are on rod C by the end. The additional constraint is that no ring of larger size can be placed on a smaller ring. In the diagram, ring \(2\) cannot be placed on ring \(1\) for example. Sounds simple, yet if it were we would not be discussing it here!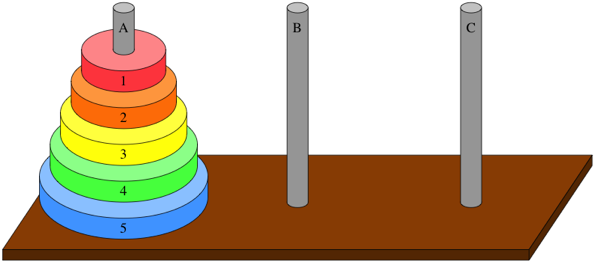 Tower of Hanoi Image

Solution

Recursive Nature of Problem

Let's start by looking at the problem with a small number of rings. If we have 1 ring, we can simply move it from rod A to rod C. If we have 2 rings, we can move the top ring from rod A to rod B, then move the bottom ring from rod A to rod C, and finally move the top ring from rod B to rod C. If we have 3 rings, we can move the top 2 rings from rod A to rod B, then move the bottom ring from rod A to rod C, and finally move the top 2 rings from rod B to rod C. Can you spot a certain pattern?

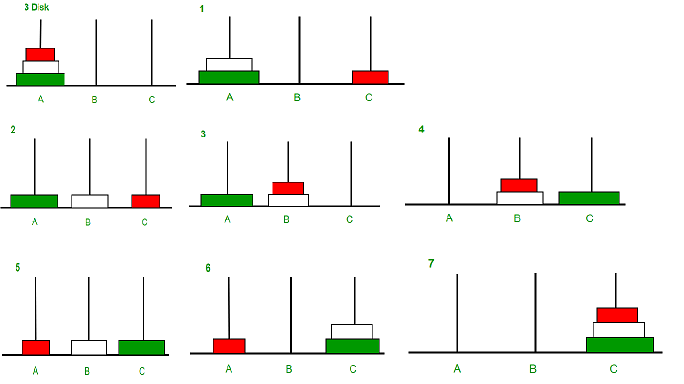
Step by step nature to Tower of Hanoi

First observe the 3rd disk (disk on bottom) in the diagram above. We know this disk must be at the bottom of rod C. In order to do this, we need all other disks not on rod C. This means we want disk 1 and 2 on rod B. Notice this is because if we were able to move disk 3 to rod C, while all other disks can remain on rod 1 without all being placed on rod 2, the problem would be trivial. Now we can apply the same logic to disk 2. We want disk 2 on rod C, so we need disk 1 on rod A. Finally, we can move disk 2 to rod C. Through the power of recursive thinking, we have created a simple procedure where we move our top n-1 disks to rod B, move our bottom disk to rod C, and finally move our top n-1 disks to rod C. Then the next step, we can apply the same logic to the top n-1 disks on rod B and move n-2 disks to rod A and so on. This is the recursive nature of the problem.

SML Solution

Given the recursive nature of this problem, this makes SML a great fit to write our solution in (this is just a personal preference). We first need to define our base case. The trival case \(n=0\) will simply return a blank statement, but this case is irrelevant for all nontrivial cases. The base case we care about is \(n=1\). In this case, we simply want to move the top disk from rod A to rod C. Now we can define our recursive case. We want to move the top n-1 disks from rod x to rod y , move the bottom disk from rod x to rod z, and finally move the top n-1 disks from rod y to rod z.

We can define this in SML as follows:

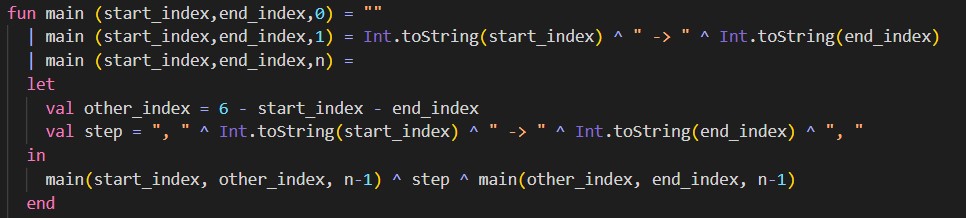
SML Solution to Tower of Hanoi

Now we can test our solution. We can define a function with \(n=10\) disks with the function call main(1,3,10). As you can see, the number of steps required increases rapidly.

Code output for main(1,3,10)

Work-Span Analysis

If you are unfamiliar with computing runtime formally, I recommend starting on page 8 of 15-251 Notes.

To analyze the runtime we will refer to the code above. For the base case of our computation, notice that it requires constant time, we will denote this as \(c_0\).

Work:

\begin{align*} W(1) &= c_0 \\ W(n) &= 2W(n-1)+c_1 \\ \end{align*}

  • Number of levels: \(n\)
  • Nodes per level: \(2^{i-1}\)
  • Work per Node: \(c_1\)
This results in the following summation:

\[\sum_{i=1}^n 2^{i-1} = 2^{n}-1 \in O(2^n) \tag{Finite Geometric Sum}\]

Span:

\begin{align*} S(1) &= c_0 \\ S(n) &= S(n-1) + c_1\end{align*}

  • Number of levels: \(n\)
  • Nodes per level: \(1\)
  • Work per Node: \(c_1\)

\[\sum_{i=1}^n c_1 = n \in O(n) \tag{Finite Geometric Sum}\]

An interesting thing is that this is the best time complexity we can acheive is exponential as that is the number of moves that must be made. Thus, our algorithm is in \(\Omega(2^n)\) and \(O(2^n)\) so the intrinsic time complexity of the Tower of Hanoi problem is \(\Theta(2^n)\). Note: Our work calculation matches our emprical results. Try counting the number of moves required given \(n\) rings, it precisely follows \(2^{n}-1\).

Citations

  • “15-251 Notes.” 15-251 Notes, Carnegie Mellon University, 2019, https://www.cs251.com/
  • De Brabandere, Sabine. “The Tower of Hanoi.” Scientific American, 26 Oct. 2017, https://www.scientificamerican.com/article/the-tower-of-hanoi/#:~:text=The%20tower%20of%20Hanoi%20(also,mental%20discipline%20of%20young%20priests.
  • "Towers of Hanoi: A Complete Recursive Visualization." Youtube, uploaded by Reducible. 26 May. 2020, https://youtu.be/rf6uf3jNjbo